2.7 Anomalous symmetry and 1D SPT
2.7.1 Symmetry Protected Topological Phase
Before moving to the quantum anomaly in QFT, here let us see the crucial connection between quantum anomaly and symmetry protected topological phase(SPT), introduced in [10], a topic in condensed-matter physics. The relationship is summarized as the following hypothesis 10
Hypothesis 2.1 (SPT-inflow hypothesis) A \(d+1\)-dimensional QFT with an anomalous global symmetry \(G\) (and non-anomalous Lorentz symmetry) can be realized as a boundary of a \((d+1)+1\)-dimensional SPT phase with (non-anomalous) symmetry \(G\).
This is a refinement of the Callan-Harvey anomaly-inflow principle [11]. Callan-Harvey anomaly-inflow asserts that a quantum anomaly is related to a classical action of backgrounds in \((d+1)+1\) dimension, but what kind of backgrounds/action can consist an “inflow action” was unclear; now it is replaced by “SPT”, which has moth more clear definition and physical interpretation.
We define the SPT on a lattice. To define, first we define the notion of “short range entangled” state.[^inv] [^conti]
Kazama-san and Yamashita-san (and probably others) pointed out a significant error in the earlier version in the lecture, so the rest of this paragraph is currently omitted. KO thanks those who corrected me.
2.7.2 Example of 1+1d SO(3) SPT
Let us construct an example of SPT on 1+1d lattice for symmetry \(SO(3)\). We put two qubits, labeled by \(A\) and \(B\), on each site. So \(\mathcal{H}_i = \mathcal{H}^A_i \otimes \mathcal{H}^B_i\), with \(\mathcal{H}^A_i \cong \mathcal{H}^B_i \cong \mathbb{C}^2\). As a on-site Let \(\ket{s_i}\) be the Bell state between the \(A\)-qubit at site \(i\) (\(i\in\mathbb{Z}\)) and the \(B\)-qubit at site \(i+1\): \(\ket{s_i} = \ket{\uparrow_{i,B}}\ket{\uparrow_{i+1,A}} + \ket{\downarrow_{i,B}} \ket{\downarrow_{i+1,A}} \in \mathcal{H}_{i}^A\otimes \mathcal{H}_{i+1}^B\). Then we define the total state \(\ket{\psi}\) by11 \[\begin{equation} \tag{2.49} \ket{\psi} = \bigotimes_i \ket{s_i}. \end{equation}\] The entanglement structure of this state is depicted in Figure 2.1. Note that, although (2.49) is defined by the tensor product, each \(\ket{s_i}\) is not contained in a single site Hilbert space \(\mathcal{H}_i\), and thus \(\ket{\psi}\) is not a tensor product of local states, each in \(\mathcal{H}_i\).
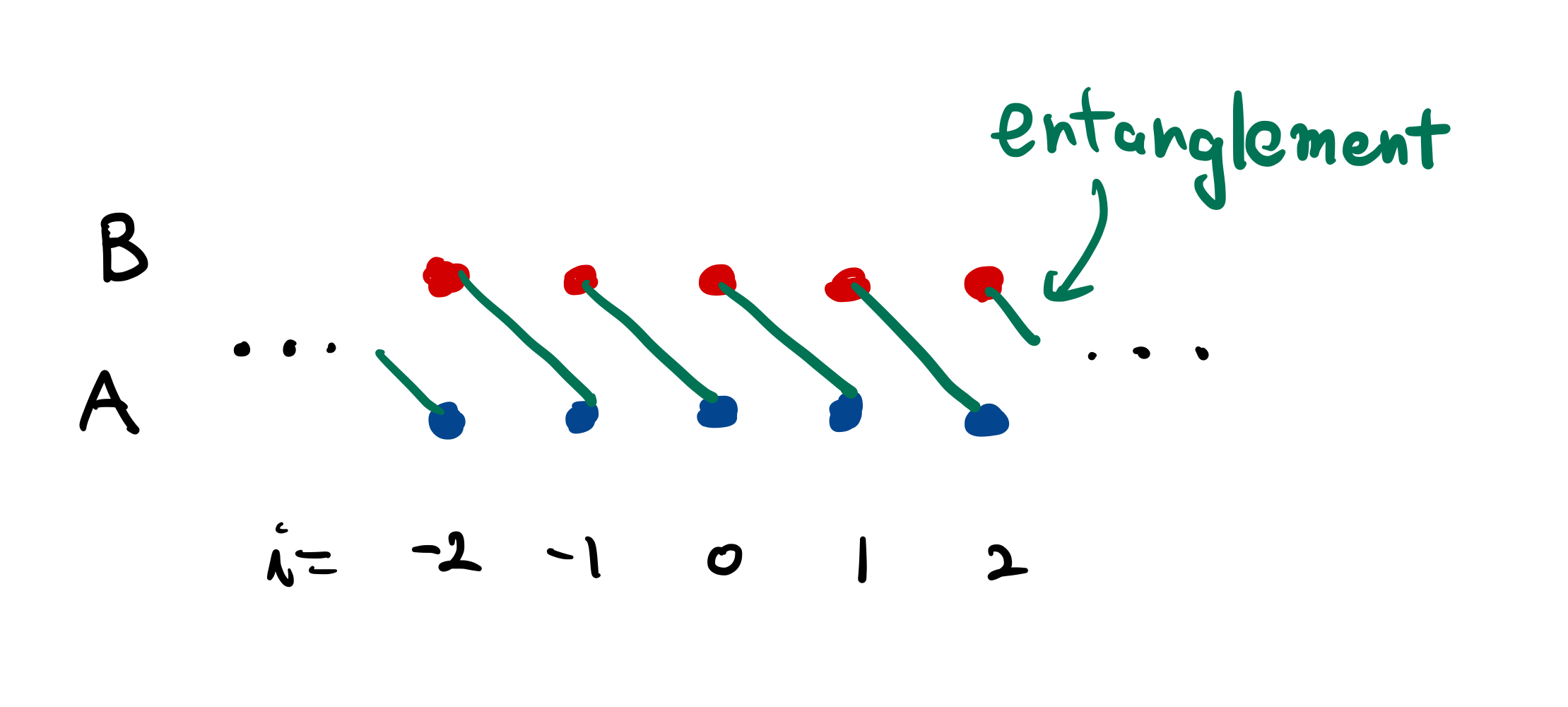
Figure 2.1: The entanglement structure of the state \(\ket{\psi}\) defined in (2.49). The \(B\)-qubit at site \(i\) is entangled with the \(A\)-qubit at side \(i+1\), as indicated by the green line.
We let the group \(SO(3)\) acts on the (projective space of) total states as follows. Let \(T_g^{(i,A)}\) and \(T_g^{(i,B)}\) be the \(SO(3)\) symmetry transformation, defined in Section @ref{Bloch}, on the \(A\)- or \(B\)-qubit at the \(i\)-th site. Then the \(SO(3)\) action for which \(\ket{\psi}\) is in SPT is \[\begin{equation} \tag{2.50} T_g = \prod_{i}T_g^{(i,A)}T_{g^{-1}}^{(i,B)}. \end{equation}\] The state \(\ket{\psi}\) is invariant under this transformation, because \(T_g = \prod_i T_{g^{-1}}^{(i,B)}T_g^{(i+1,A)}\) and \(T_{g^{-1}}^{(i,B)}T_{g}^{(i+1,A)}\) makes the singlet state \(\ket{s_i}\) invariant. Note that this symmetry transformation does not have the projective phase: it is cancelled between the ones coming from \(U_g^{(i,A)}\) and \(U_{g^{-1}}^{(i,B)}\) within each site.
The direct exposition that \(\ket{\psi}\) is in a SPT can be found in [13]. Here instead we observe how the Hypothesis 2.1 works in this example. The state \(\ket{\psi}\) has no problem to be defined on a periodic lattice. However, when there is a boundary, say that only \(i \in \mathbb{Z}_{\ge 0}\) participate in the lattice, the \(A\)-qubit at site \(i=0\) does not have its partner to create an entanglement. Thus, there are equally good/bad extensions of the state \(\ket{\psi}\) to open boundary: \[\begin{equation} \tag{2.51} \ket{\uparrow,\psi} = \ket{\uparrow_{0,A}}\otimes \bigotimes_{i\ge 0}\ket{s_{i}}, \quad \ket{\downarrow,\psi} = \ket{\downarrow_{0,A}}\otimes \bigotimes_{i\ge 0}\ket{s_{i}}. \end{equation}\] We call the degrees of freedom \(\ket{\uparrow \! \downarrow_{0,A}}\) the edge modes, as it localizes at the boundary. On this edge mode, the \(SO(3)\) symmetry acs by \(T_g\), which is exactly the projective representation the qubit has. This edge mode is robust – if you force the \((i=0,A)\)-qubit be entangled with another qubit (in a finite distance) by some unitary, you get another unentangled qubit, as you cannot erase/create the entanglement by unitaries. In summary, if we cut the chain in the SPT, on the edge we have the qubit protected by the projective action of \(SO(3)\).
2.7.3 SPT for a general projective representation*
It is easy the generalize the above example into a general projective representation \(R\) of a group \(G\). (Here we assume that \(G\) acts by unitary operations.) For each site we prepare the local Hilbart space as \(\mathcal{H}_i = R_i \otimes R^\vee_i\), where \(R_i\) is the \(i\)-th copy of \(R\) and \(R^\vee_i\) is the dual of \(R\). Pick a basis \(\ket{i}\) in \(R\), let \(\ket{i^\vee} \in R^\vee\) denote the dual basis, and then define the singlet state \(\ket{s_i}\) by \[\begin{equation} \tag{2.52} \ket{s_i} = \sum_{i}^{\mathrm{dim}R} \ket{i^\vee}\otimes\ket{i}\in R_{i}^\vee \otimes R_{i+1}. \end{equation}\] This state is invariant under \(T_{g^{-1}}^{(i,B)}T_g^{(i+1,A)}\) (and nonzero). Now the rest of the constuction is the same as above, and we see the edge mode in \(R\) when the lattice has a boundary. Thus we have seen how the (one direction of) Hypothesis 2.1 works in the 1+1d bulk/0+1d boundary case.
References
The name of the hypothesis is cooked up by KO. Also the correct reference is not clear to KO (other than having a very long list); it feels more like a theme that gradually arose over a time (through the decade of 2010).↩︎
This state looks very artificial. Instead, on can consider the state \[\begin{equation*} \ket{\mathrm{AKLT}} = \prod_i P_i^\text{triplet} \ket{\psi} \end{equation*}\] where \(P_i^\text{triplet}\), acting on \(\mathcal{H}_i\), is the projection operator onto the triplet states consists of the \(A\)- and \(B\)- qubits on the same site \(i\). This state ,in the same SPT as \(\ket{\psi}\), is the ground state of the AKLT Hamiltonian defined with spin-1 operators \(\vec{S}_i\) [12]: \[\begin{equation*} H_{\mathrm{AKLT}} = \sum_i \Bigl(\vec{S}_i \cdot \vec{S}_{i+1} + \frac13 \bigl(\vec{S}_{j} \cdot \vec{S}_{j+1}\bigr)^2\Bigr), \end{equation*}\] which was studied way before the invention the notion of SPT.↩︎